진법
진법
진법이란 수를 표기하는 기수법의 하나로 임의의 숫자를 사용하여 수를 표현하는 방법입니다.
우리가 일반적으로 사용하는 1부터 9까지의 숫자를 사용하여 수를 나타내는 방법은 10진법이라고 부릅니다.
현재 프로그래밍에서 많이 사용되고 있는 진법은 다음과 같습니다.
1. 2진법
2. 8진법
3. 10진법
4. 16진법
특히 모든 데이터가 0과 1로 저장되는 컴퓨터의 특성 상 2진법은 컴퓨터 구조 및 동작을 이해하는 데 아주 중요한 역할을 합니다.
2진법(binary notation)
2진법은 0과 1, 두 개의 숫자만으로 수를 표현하는 방법입니다.
이러한 2진수는 자릿값이 올라감에 따라 그 크기가 2배씩 커지게 됩니다.
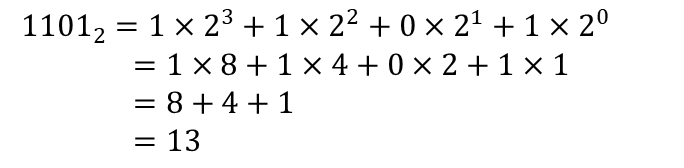
8진법(octal notation)
8진법은 0부터 7까지의 숫자로 수를 표현하는 방법입니다.
이러한 8진수는 2진수를 3자리씩 빠르게 묶어 표현할 수 있어, 비트 단위까지 신경쓰며 프로그래밍을 하던 초창기 컴퓨터에서 많이 사용했습니다.
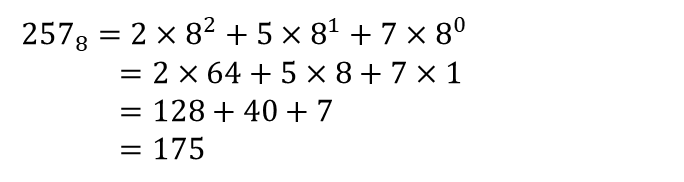
10진법(decimal notation)
10진법은 0부터 9까지의 숫자로 수를 표현하는 방법으로, 우리가 일상 생활에서 수를 나타낼 때 흔히 사용하는 방법입니다.
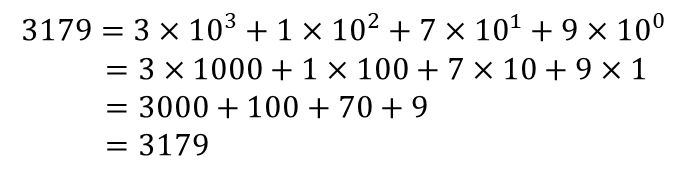
16진법(hexadecimal notation)
16진법은 0부터 9까지의 숫자와 A부터 F까지의 문자를 함께 사용하여 수를 표현하는 방법입니다.
이러한 16진수는 특히 컴퓨터 분야에서 1바이트(byte)의 크기를 쉽게 표현할 수 있어 많이 사용되고 있습니다.
0부터 9까지는 10진수와 동일하며, 10부터 15까지는 다음과 같이 영문자로 나타냅니다.
| A | B | C | D | E | F |
|---|---|---|---|---|---|
| 10 | 11 | 12 | 13 | 14 | 15 |
따라서 16진수는 자릿수 하나로 0부터 15까지를 표현할 수 있게 됩니다.
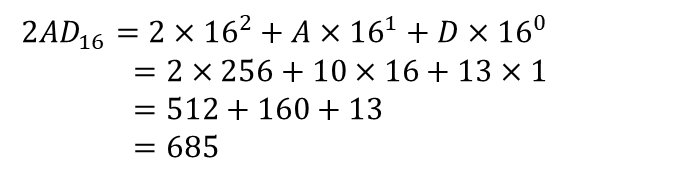
진법 변환
10진수를 각 진법으로의 변환하는 방법은 다음과 같습니다.
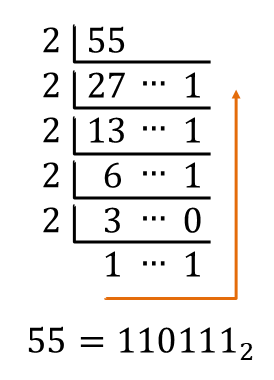
1. 10진수를 변환하고자 하는 진법의 기수(2진법이면 2가 기수임)로 나누고, 해당 나머지를 기록합니다.
2. 나눈 몫을 또 다시 변환하고자 하는 진법의 기수로 나누고, 해당 나머지를 기록합니다.
3. 이렇게 계속해서 나눈 몫을 기수로 나누다가 나눈 몫이 해당 기수보다 작아지면 중단합니다.
4. 마지막 몫과 지금까지 기록한 나머지들을 역으로 연결하면 해당 진법의 수가 완성됩니다.
예제) 10진수 55를 2진수로 변환하시오.
진법별 표현 비교
| 10진법 | 2진법 | 8진법 | 16진법 | 10진법 | 2진법 | 8진법 | 16진법 |
|---|---|---|---|---|---|---|---|
| 0 | 0000 | 0 | 0 | 8 | 1000 | 10 | 8 |
| 1 | 0001 | 1 | 1 | 9 | 1001 | 11 | 9 |
| 2 | 0010 | 2 | 2 | 10 | 1010 | 12 | A |
| 3 | 0011 | 3 | 3 | 11 | 1011 | 13 | B |
| 4 | 0100 | 4 | 4 | 12 | 1100 | 14 | C |
| 5 | 0101 | 5 | 5 | 13 | 1101 | 15 | D |
| 6 | 0110 | 6 | 6 | 14 | 1110 | 16 | E |
| 7 | 0111 | 7 | 7 | 15 | 1111 | 17 | F |






