딥러닝에서 사용되는 알고리즘
심층 신경망
다양한 종류의 심층 신경망 구조가 존재하지만, 대부분의 경우 대표적인 몇 가지 구조들에서 파생된 것이다. 그렇지만 여러 종류의 구조들의 성능을 동시에 비교하는 것이 항상 가능한 것은 아닌데, 그 이유는 특정 구조들의 경우 주어진 데이터 집합에 적합하도록 구현되지 않은 경우도 있기 때문이다.
심층 신경망(Deep Neural Network, DNN)
심층 신경망(Deep Neural Network, DNN)은 입력층(input layer)과 출력층(output layer) 사이에 여러 개의 은닉층(hidden layer)들로 이뤄진 인공신경망(Artificial Neural Network, ANN)이다. 심층 신경망은 일반적인 인공신경망과 마찬가지로 복잡한 비선형 관계(non-linear relationship)들을 모델링할 수 있다.
예를 들어, 사물 식별 모델을 위한 심층 신경망 구조에서는 각 객체가 이미지 기본 요소들의 계층적 구성으로 표현될 수 있다. 이때, 추가 계층들은 점진적으로 모여진 하위 계층들의 특징들을 규합시킬 수 있다. 심층 신경망의 이러한 특징은, 비슷하게 수행된 인공신경망에 비해 더 적은 수의 유닛(unit, node)들 만으로도 복잡한 데이터를 모델링할 수 있게 해준다.
이전의 심층 신경망들은 보통 앞먹임 신경망으로 설계되어 왔지만, 최근의 연구들은 심층 학습 구조들을 순환 신경망(Recurrent Neural Network, RNN)에 성공적으로 적용했다. 일례로 언어 모델링(language modeling) 분야에 심층 신경망 구조를 적용한 사례 등이 있다.
합성곱 신경망(Convolutional Neural Network, CNN)의 경우에는 컴퓨터 비전(computer vision) 분야에서 잘 적용되었을 뿐만 아니라, 각각의 성공적인 적용 사례에 대한 문서화 또한 잘 되어 있다. 더욱 최근에는 합성곱 신경망이 자동 음성인식 서비스(Automatic Response Service, ARS)를 위한 음향 모델링(acoustic modeling) 분야에 적용되었으며, 기존의 모델들 보다 더욱 성공적으로 적용되었다는 평가를 받고 있다.
심층 신경망은 표준 오류역전파 알고리즘으로 학습될 수 있다. 이때, 가중치(weight)들은 아래의 등식을 이용한 확률적 경사 하강법(stochastic gradient descent)을 통하여 갱신될 수 있다.
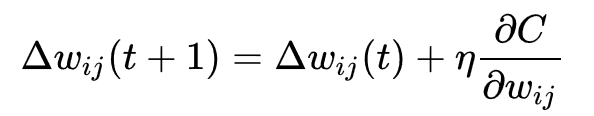
여기서, η는 학습률(learning rate)을 의미하며, C는 비용함수(cost function)를 의미한다. 비용함수의 선택은 학습의 형태(지도 학습, 자율 학습 (기계 학습), 강화 학습 등)와 활성화함수(activation function)같은 요인들에 의해서 결정된다. 예를 들면, 다중 클래스 분류 문제(multiclass classification problem)에 지도 학습을 수행할 때, 일반적으로 활성화함수와 비용함수는 각각 softmax 함수와 교차 엔트로피 함수(cross entropy function)로 결정된다.
softmax 함수는
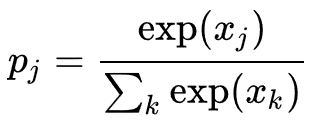
로 정의된다, 이때, Pj 는 클래스 확률(class probability)을 나타내며, Xj 와 Xk 는 각각 유닛 j로의 전체 입력(total input)과 유닛 k 로의 전체 입력을 나타낸다. 교차 엔트로피는
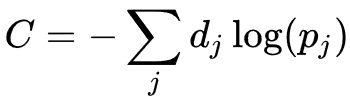
로 정의된다, 이때, dj 는 출력 유닛 j 에 대한 목표 확률(target probability)을 나타내며, Pj 는 해당 활성화함수를 적용한 이후의 j 에 대한 확률 출력(probability output)이다.
심층 신경망의 문제점
기존의 인공신경망과 같이, 심층 신경망 또한 나이브(naive)한 방식으로 학습될 경우 많은 문제들이 발생할 수 있다. 그 중 과적합과 높은 시간 복잡도가 흔히 발생하는 문제들이다.
심층 신경망이 과적합에 취약한 이유는 추가된 계층들이 학습 데이터의 rare dependency의 모형화가 가능하도록 해주기 때문이다. 과적합을 극복하기 위해서 weight decay (l2–regularization) 또는 sparsity (l1–regularization) 와 같은 regularization 방법들이 사용될 수 있다. 그리고 최근에 들어서는 심층 신경망에 적용되고 있는 정규화 방법 중 하나로 dropout 정규화가 등장했다. dropout 정규화에서는 학습 도중 은닉 계층들의 몇몇 유닛들이 임의로 생략된다. 이러한 방법은 학습 데이터(training data)에서 발생할 수 있는 rare dependency를 해결하는데 도움을 준다.
오차역전파법과 경사 하강법은 구현의 용이함과 국지적 최적화(local optima)에 잘 도달한다는 특성으로 인해 다른 방법들에 비해 선호되어온 방법들이다. 그러나 이 방법들은 심층 신경망을 학습 시킬 때 시간 복잡도가 매우 높다. 심층 신경망을 학습시킬 때에는 크기(계층의 수 와 계층 당 유닛 수), 학습률, 초기 가중치 등 많은 매개변수(parameter)들이 고려되어야 한다. 하지만 최적의 매개변수들을 찾기 위해 매개변수 공간 전부를 확인하는 것은 계산에 필요한 시간과 자원의 제약으로 인해 불가능하다. 시간 복잡도를 해결하기 위해, 미니 배치(mini batch, 여러 학습 예제들의 경사를 동시에 계산), 드롭 아웃(drop out)과 같은 다양한 '묘책’들이 등장하였다. 또한, 행렬 및 벡터 계산에 특화된 GPU는 많은 처리량을 바탕으로 두드러지는 학습 속도 향상을 보여주었다.






