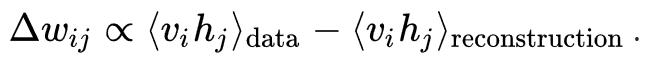딥러닝에서 사용되는 알고리즘
제한 볼츠만 머신 (Restricted Boltzmann Machine, RBM)
볼츠만 머신에서, 층간 연결을 없앤 형태의 모델이다. 층간 연결을 없애면, 머신은 가시 유닛(Visible Unit)과 은닉 유닛(Hidden Unit)으로 이루어진 무방향 이분 그래프 형태의 모양이 된다. 결론적으로 모델의 층간 연결을 없앰으로써, 얻는 이점으로 뉴럴 네트워크는 깊어질 수 있었다. 가장 큰 이점은 가시 유닛이 관찰되고 고정(Clamped)되었을 때 은닉 유닛을 추론(Inference) 하는 MCMC 과정이 단 한 번에 끝난다는 것이다.
RBM은 확률모델의 계산이 불가능하기 때문에, 학습시 근사법인 MCMC 나 또는 제프리 힌튼 교수가 발견한 CD(Contrastive Divergence) 를 사용하는데, RBM의 모델의 간단함에서 오는 추론에 대한 이점은 샘플링 근간의 학습법이 실용적인 문제에 적용되는데 기여했다. 자세한 학습 방법은 아래에 설명 되어 있다.
RBM은 DBN의 기본 뼈대가 된다, RBM을 쌓아올리면서(Stacking), Greedy하게 학습함으로써, DBN을 완성한다. DBN을 아는 사람은 기본적으로 RBM은 무방향이기에, RBM이 방향성 있는 모델인 DBN이 되는지 의아할 것이다. 이는 제프리 힌튼 의 제자인 Teh, Y. W 의 우연 발견적인 연구 성과인데, 원래 힌튼 교수는 Graphical Model 이 방향성을 가질 때 생기는 Explaining Away 효과 때문에 학습이 매우 어려워 연구를 무방향성 모델로 선회했다가, RBM을 쌓으면, 다층 RBM이 되는 것이 아니라, DBN과 비슷해진다는 사실을 발견하게 된다. 이 발견은 DBN학습을 단순히 여러 개의 RBM 학습으로 환원시킴으로써(앞서서 얘기했듯이 RBM은 학습이 어렵지 않다) 어려운 DBN 학습의 복잡도를 층의 갯수에 비례하는 복잡도로 낮추었다. 이는 선행학습(Pre-training) 과 미세조정(fine-tuning) 의 새로운 학습 패러다임으로 발전하게 된다.
RBM 훈련 과정에서의 가중치 갱신은, 다음의 식을 기반으로 경사 하강법을 통해 이루어진다.
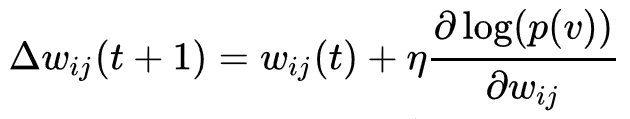
여기서 p(v) 는 다음의 식으로 주어지는 가시 벡터의 확률을 나타내고,
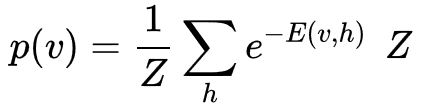
는 정규화를 위해 사용되는 분배함수(partition function)이며, E(v, h) 는 신경망의 상태(state)에 부여되는 에너지 함수이다. 에너지가 낮을수록 해당 신경망이 더 적합한 상태임을 의미한다. 기울기
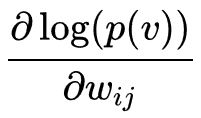
는 좀 더 간단하게
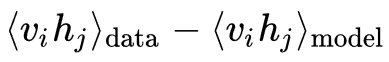
로 표현이 되는데 이 때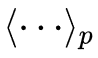 
는 분포 p 에 관한 평균을 의미한다. 
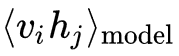을 샘플링 하려면 alternating Gibbs sampling을 매우 많이 반복해야 하기 때문에 CD에서는 alternating Gibbs sampling을 n 회만 반복한다.(실험을 통해 n = 1 일 경우에도 충분한 성능이 나온다고 알려져 있다).
n 회 반복 후 샘플링 된 데이터가
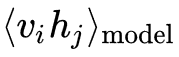
를 대신한다. CD 수행 과정은 다음과 같다:
1. 가시 유닛들을 훈련 벡터로 초기화 한다.
2. 다음의 가시 유닛들이 주어지면 은닉 유닛들을 모두 동시에 갱신한다:
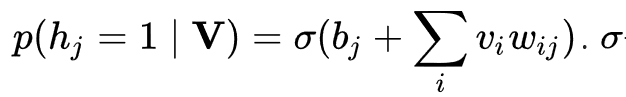
는 시그모이드 함수(sigmoid function)를 의미하며,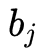 
는 
의 편향이다.
3. 다음의 은닉 유닛들이 주어지면 가시 유닛들을 모두 동시에 갱신한다:
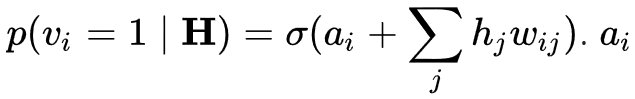
는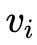 
의 편향이다. 이 부분을 "복원(reconstruction)"이라고 부른다.
4. 복원된 가시 유닛들이 주어지면 2 에서 쓰인 식을 이용하여 은닉 유닛들을 모두 동시에 다시 갱신한다.
5. 다음과 같이 가중치를 갱신한다.
