최대공약수와 최소공배수
최대공약수(Greatest Common Divisor, GCD)
공약수(common divisor)란 두 수 이상의 여러 수의 공통된 약수를 의미합니다.
최대공약수(GCD)란 두 수 이상의 여러 수의 공약수 중 최대인 수를 가리킵니다.
최대공약수
두 수 a, b의 최대공약수는 gcd(a, b) 또는 (a, b)로 나타냄.
예제) 72와 90의 최대공약수를 구하시오.
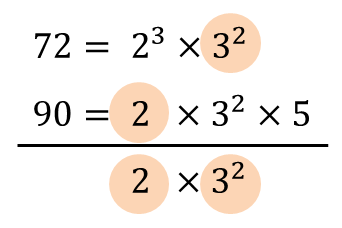
∴ gcd(72, 90) = 2 x 32 = 18
만약 gcd(a, b) = 1이면, 두 수 a, b는 서로소(coprime) 관계에 있다고 합니다.
최대공약수와 최소공배수에 대한 더욱 자세한 내용은 중학교 1학년 수학 과목에서 배우실 수 있습니다.
최소공배수(Lowest Common Multiple, LCM)
공배수(common multiple)란 두 수 이상의 여러 수의 공통된 배수를 의미합니다.
최소공배수(LCM)란 두 수 이상의 여러 수의 공배수 중 최소인 수를 가리킵니다.
최소공배수
두 수 a, b의 최소공배수는 lcm(a, b) 또는 [a, b]로 나타냄.
예제) 24와 30의 최소공배수를 구하시오.
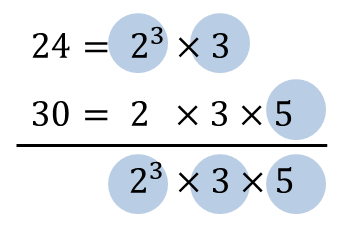
∴ lcm(24, 30) = 23 x 3 x 5 = 120






