수열
수열(sequence)
수열(sequence)이란 자연수를 정의역으로 갖는 함수나 그 함수의 결과로 얻어지는 원소들을 나열한 것을 의미합니다.
수열을 이루고 있는 각 수를 항(term)이라고 하며, 순서대로 첫째 항(첫항), 둘째 항, 셋째 항 등으로 읽습니다.
또한, 특정되지 않은 임의의 항을 제 n항이라고 부르며, 이것을 수열의 일반항이라고 합니다.
만약 수열이 일정한 규칙을 가질 경우 그 규칙에 따라 등차수열, 등비수열 등으로 구분할 수 있습니다.
이러한 수열은 원소가 순서를 가지며, 중복이 허용된다는 점에서 집합과는 구별됩니다.
수열의 표현
1. 수열의 항을 순서대로 나열하여 표현 : {1, 3, 5, 7, ...} 또는 (1, 3, 5, 7, ...)
2. 일반항으로 표현가능한 경우 : {2n - 1}
위의 두 수열은 모두 홀수의 수열을 가리키는 수열의 표현입니다.
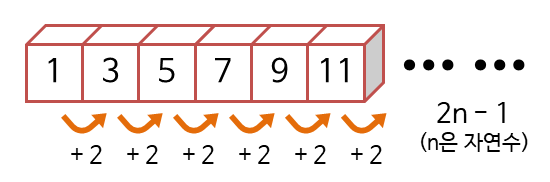
등차수열(arithmetic sequence)
등차수열(arithmetic sequence)이란 연속하는 두 항의 차이가 모두 일정한 수열을 가리킵니다.
이때 두 항의 차이는 이 수열의 모든 항에 대해서 공통적으로 나타나는 차이이므로 공차(common difference)라고 부릅니다.
예를 들어, 앞서 살펴본 홀수의 수열은 첫항이 1이고, 공차가 2인 등차수열인 것입니다.
예제) 첫항이 4이고 공차가 3인 등차수열은 다음과 같이 표현할 수 있습니다.
풀이) { 4, 7, 10, 13, 16, 19, ... } 또는 { 3n+1 }
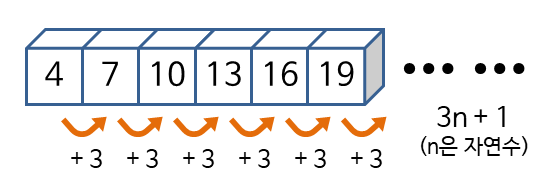
등비수열(geometric sequence)
등비수열(geometric sequence)이란 수열의 각 항이 그 앞의 항에 일정한 수를 곱한 것으로 이루어진 수열을 가리킵니다.
따라서 첫항은 0이 되어서는 안되며, 곱하는 일정한 수를 공비(common ratio)라고 부릅니다.
등비수열
첫항이 a이며, 공비가 r인 등비수열의 n번째 항은 다음과 같습니다.
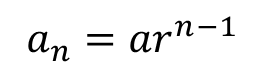
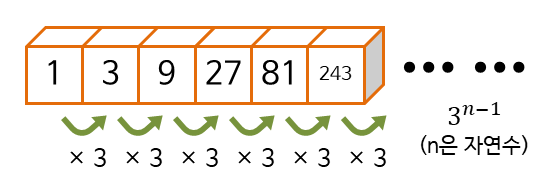
예제) 첫항이 1이고 공비가 3인 등비수열은 다음과 같이 표현할 수 있습니다.
: { 1, 3, 9, 27, 81, 243, 729, ... } 또는 { 3n-1 }
예제) 첫항이 4이고 공비가 -1인 등비수열은 다음과 같이 표현할 수 있습니다.
: { 4, -4, 4, -4, 4, -4, 4, ... } 또는 { 4(-1)n+1 }






