명제
명제(proposition)
명제(proposition)란 그 내용이 참인지 거짓인지를 누구나 명확하게 판단할 수 있는 식이나 문장을 의미합니다.
예제) 서울은 대한민국의 수도이다. : 참인 명제
예제) 파리는 미국의 수도이다. : 거짓인 명제
예제) 빨간색은 이쁘다. : 참과 거짓을 판단할 수 없으므로 명제가 아님.
명제
어떤 명제가 'p이면 q이다.’의 형태로 표현될 때,
p를 가정, q를 결론이라고 하며, 기호로는 p → q와 같이 나타냄.
명제에서 부정은 '~'기호로 표현합니다.
역, 이, 대우
원 명제의 가정과 결론을 바꾸어 놓은 명제를 해당 명제의 역(逆)이라고 합니다.
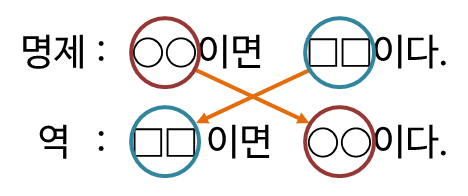
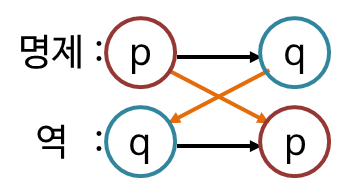
그리고 원 명제의 가정과 결론을 각각 부정한 명제를 해당 명제의 이(裏)라고 합니다.
마지막으로 원 명제의 역(逆)의 가정과 결론을 각각 부정한 명제를 해당 명제의 대우(對偶)라고 합니다.
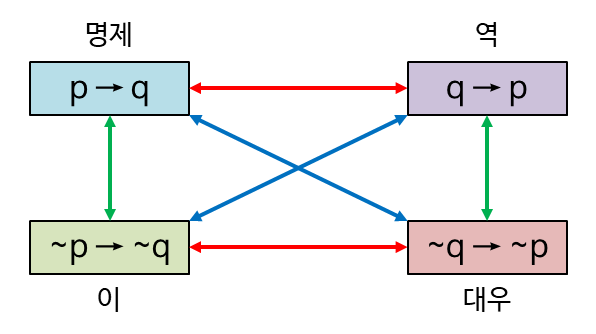
위의 그림에서 빨간색 화살표는 역, 초록색 화살표는 이, 파란색 화살표는 대우 관계를 나타냅니다.
원 명제와 역과 이, 그리고 대우 사이에는 다음과 같은 관계가 성립합니다.
1. 원 명제와 그 명제의 대우는 언제나 같은 불리언 값을 가집니다.
예제)
명제 : 숫자 a가 짝수이면, 3a는 짝수이다. (참)
대우 : 3a가 짝수가 아니면, 숫자 a는 짝수가 아니다. (참)
2. 원 명제의 역과 이는 언제나 같은 불리언 값을 가집니다.
예제)
명제 : 두 삼각형이 합동이면, 두 삼각형의 넓이는 같다. (참)
역 : 두 삼각형의 넓이가 같으면, 두 삼각형은 합동이다. (거짓)
이 : 두 삼각형이 합동이 아니면, 두 삼각형의 넓이는 같지 않다. (거짓)






