삼각함수
삼각함수(trigonometric function)
삼각함수(trigonometric function)란 각에 대한 함수로 삼각형의 각과 변의 길이를 서로 연관시킨 함수입니다.
이러한 삼각함수는 직각삼각형의 두 변의 길이의 비로 정의할 수 있습니다.
삼각함수에는 다음과 같은 세 개의 기본적인 함수를 정의하고 있습니다.
1. 사인(sine, 기호 sin)
2. 코사인(cosine, 기호 cos)
3. 탄젠트(tangent, 기호 tan)
또한, 이 함수들의 역수를 각각 다음과 같이 정의하고 있습니다.
1. 코시컨트(cosecant, 기호 csc)
2. 시컨트(secant, 기호 sec)
3. 코탄젠트(cotangent, 기호 cot)
직각삼각형을 이용한 삼각함수의 정의
가장 손쉽게 삼각함수를 정의하는 방법은 바로 직각삼각형을 이용하는 것입니다.
하지만 직각삼각형의 각은 0˚ 부터 90˚ 사이이므로, 직각삼각형을 이용해 정의한 삼각함수는 음의 각이나 90˚ 보다 큰 각에 대해서는 적용되지 않습니다.
∠C가 직각인 직각삼각형 ABC에서, ∠A, ∠B, ∠C의 대변(마주보는 변)의 길이를 각각 a , b , c라고 하면, 삼각함수를 다음과 같이 정의할 수 있습니다.
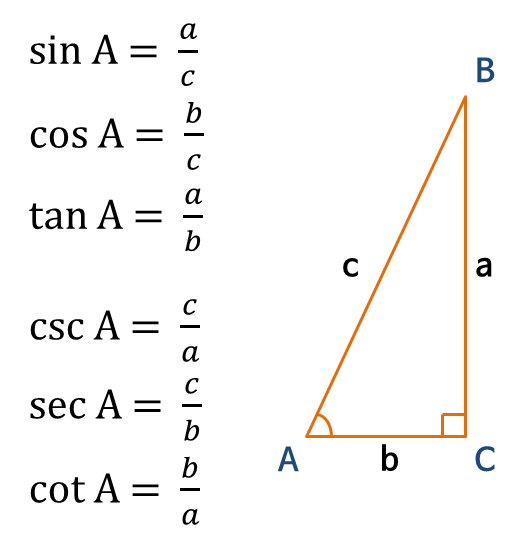
예제) 위 그림과 같이 ∠C가 직각인 직각삼각형에서 ∠A = 60, ∠B = 30, a = √3, b = 1, c = 2인 경우, ∠A에 대한 사인, 코사인, 탄젠트 함수를 각각 구하시오.
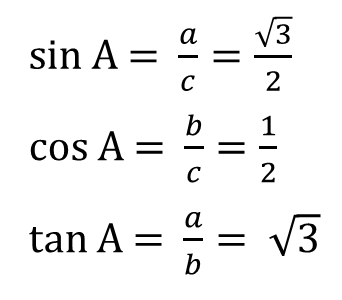
특정 각도에 대한 삼각함수 값
자주 사용되는 특정 각도에 대한 삼각함수 값을 미리 알아두면, 삼각함수를 다룰 때 편리하게 사용할 수 있습니다.
| 각도 | 사인(sin) | 코사인(cos) | 탄젠트(tan) |
|---|---|---|---|
| 0 (0˚) | 0 | 1 | 0 |
| π / 6 (30˚) | 1 / 2 | √3 / 2 | 1 / √3 |
| π / 4 (45˚) | √2 / 2 | √2 / 2 | 1 |
| π / 3 (60˚) | √3 / 2 | 1 / 2 | √3 |
| π / 2 (90˚) | 1 | 0 | ∞ |
예제) 다음 삼각함수를 구하시오.
sin 30˚ = 1 / 2
tan 60˚ = √3
cos(π / 2) = 0






